Adventure planning and decision-making using KMeans clustering

A post about solving a real everyday life problem by grouping people with similar wishes using data analysis and machine learning.

At Codecation 2019, we had an activity planned to break up the programming sessions. As a group of 17 people, it's hard to accommodate everybody's wishes so we organized a session where we voted for what we wanted to do. The poll included 8 alternatives:

🚴‍ Biking 🏖 Beach 🧗‍ Gibraltar Rock 👟 Hike (mountains) 👀 Village watching 🕵️‍ ️Escape Room 🏸 Paddle 🍷 Wine Tasting

Everybody was asked to prioritize the activities between 1 (most preferred) and 8 (least preferred). This is a powerful voting system since you can also specify what you do not want to do. Below is the distribution of votes for each activity.

We can see that nobody wanted to go biking, most people were interested in mountain hiking, and wine tasting was a typical third alternative while people had polarized views on paddle tennis.

If we were to make a decision about what activity to do based on the above plot and our intuition, it would be hiking. We can further strengthen our intuition by plotting densities for each activity:

In the above violin plot, we can see that the mean score is lowest for hiking, and there's very low standard deviation in the votes (orange horizontal line), compared to the other activities. If a violin looks like an hourglass, it means that people had polarized views on that activity.

Deciding for the entire group to go hiking would be a decision that no one can blame you for, but we can do better. For example, the same people that didn't prioritize hiking could rate the same, other activity as a priority. That would mean that no one gets upset if we split up. People were okay with splitting into two groups. But how do we make such a split?

KMeans Clustering

We will group people by how similar their choices were. By denoting each activity as a feature, and every users' vote as a value for that feature, we end up with a DataFrame like this (where every row is a specific person's vote line):

KMeans clustering will partition every person into a group, where each person belongs to the group with the closest mean of the feature vector. This means that people with similar choices would be assigned to the same cluster.

Plotting the data in 8 dimensions isn't very feasible, so after clustering and performing dimensionality reduction of our data (PCA to two dimensions), we can observe the points and cluster centroid in 2D space:

The above plot doesn't really tell you much, but it gives you an idea if the clustering worked, and where close calls were made. For example, the leftmost blue point has about the same distance to the orange and blue cluster centroids, and is probably the most likely person to switch groups, given a chance.

We can can get further insights by plotting our original data in a slightly different way, with the addition of our new-found clusters.

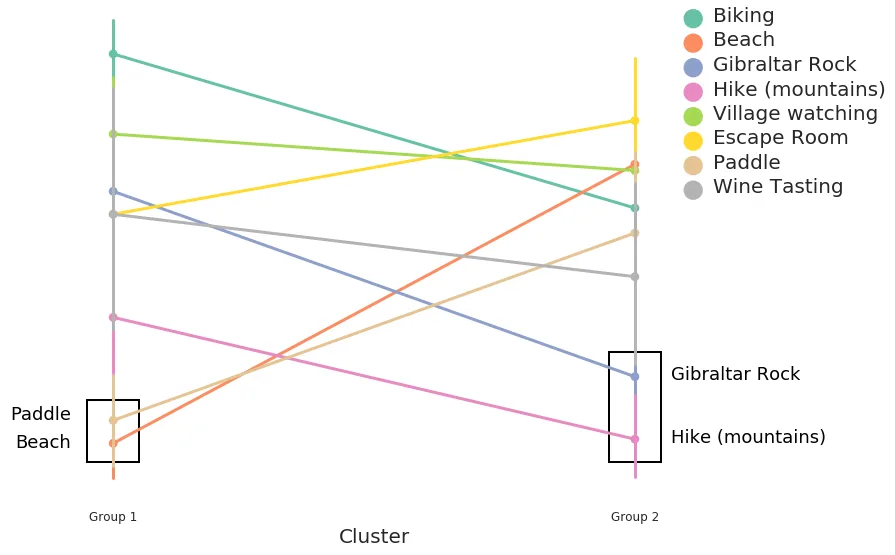Preferred activities for the two groups. Lower y-value is more preferred. Hiking places high for both groups, but isn't the most popular option for Group 1.

Voilà, we just made everybody happier. Group 1 would either go to the beach or play paddle tennis (or both!?), while Group 2 would go hiking or go to Gibraltar Rock.

Learnings, and what we end up doing

The group appreciated this analysis, and were happy with their groups. It was easy for the groups to internally decide what to do. However, as we were looking for hiking areas, we found a place for river walking in a gorge, which everybody wanted to do. As usual, you should build your analysis on data that you trust, and make sure that your data gathering method is rock solid.